I. Programming Assignments
You are
encouraged to make your programs interactive. Ideally, you should
implement them as Java applets and make them public on your web site
(It is the easiest way to evaluate them. In this case images can be
smaller than 300x300). If you prefer, you can also implement them
using C/C++ and OpenGL and post the output images in your web
site.
Note: Check often this page, specially before
you submit your assignments. All updates and the latest information
will be posted here. The URL is:
/~nis/junk/lecture/VisRep07.html
Assignment#1: Implement a program that displays Bézier curves.
Raise the degree by one and display the same Bézier curve with the control points.
Split the curve in two and display the two curves with their control points.
Make a circle with three or four rational Bézier curves.
The program should display n-degree curves. Refer to [1] and the applet on the following URL: /~nis/javaexampl/bezie.htm
You should be able to:
Assignment#2: Implement a program that solves sixth degree polynomial equations using Bézier Clipping.
Any polynomials can be converted to Bézier functions. You can specify the coefficients of a polynomial either by directly inputting them or by assigning the coordinates of the control points from the Bézier functions.
Refer to [1] or [2] for Bézier Clipping.
While a program that just displays the solutions through the console is acceptable, it is better if it can display the result visually. Refer to Assignment#1 and the following URL in order to display Bézier curves: /~nis/javaexampl/bclip/bzclip.html
Discuss the differences with other solvers such as the Newton method, and compare the computational times.
Assignment#3: Implement a program that performs ray tracing.
The program only needs to support spheres and planes as scene objects.
Refer to [3] for ray-sphere and ray-plane intersection tests.
Use Phong shading as a shading model, and suppose a parallel light source.
Add shadow computations as shown in the following image:
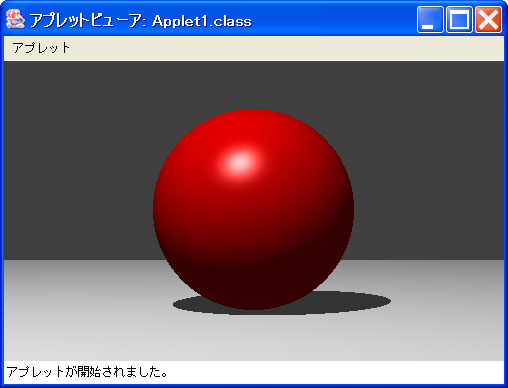
Phong shading
Assignment#4: Photorealistic images can be generated by taking the light interreflections into account. Implement a program that employs the radiosity method. For simplicity, do it in 2D only.
Compute the radiosity matrix (see [4]) for the scene above, where the numbers in the image are the indices of patches. Suppose that each patch is diffuse, the reflectance coefficient is ρ, the lengths of the patch are one, and the patches orthogonally intersect with each other at corners. Note that, while the form factor for 3D is
,
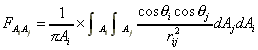the denominator is not quadratic but linear for 2D because A
represents a length for 2D while it represents an area for 3D. Also
note that π should be replaced with two for 2D.
Let L be the intensity of the light, and B be a vector of the energy for each patch. Describe B with the radiosity matrix above and L.
Compute B using the Gauss-Seidel method.
Visualize the result. For example, you can plot the graph of the intensity distribution of light on the floor.
If you do not have time to learn Java or X-Window APIs, you can visualize the result as follows: compute the color for each screen pixel and store it into an array with the same size as the screen. Then dump the array into a file and visualize the file with some external viewer or tool. About 500x400 would be appropriate for the size of images. In this case, you must submit the source code and the hard copy of the result (printed on paper).
References
[1] Resume for Oct. 21
[2] Nishita et al. "Ray Tracing Trimmed Rational Surface Patches" (Proc. of SIG90)
[3] Resume for Nov. 29
[4] Resume for Dec. 13
II. Report Assignments
Derive the procedure to convert n-degree polynomials into n-degree Bézier curves.
Solve the following problems with respect to Bézier curves:
Prove the fact that multiplying an n-degree Bézier function by an m-degree Bézier function generates a Bézier function. What is the degree of the resultant Bézier function?
Derive a formula to compute the control points and weights in order to represent a parabola with a quadratic rational Bézier curve.
Derive a formula to compute the intersection point with a line L and a quadratic Bézier surface C. Compute the normal at the intersection point.
Describe the most important factors to obtain photorealistic CG images of natural phenomena.
Explain the photon mapping method, and describe the effects obtained using the method.
Choose a notable contributor to the computer graphics community who has received award(s) from SIGGRAPH and explain his/her contribution.
Deadline: Feb. 15 (Fri.) Submit the results by: publishing them on your web site, sending them via email, or printing and handing a hard copy to the department office. (Science Building#7, 1st floor: Mrs. Tamura).
Contact: email: nis@is.s.u-tokyo.ac.jp, Phone: Extension 24106 (Nishita Lab.), URL: /~nis/