５.1 直線の描画

ラスタスキャン方式のディスプレイでは、直線は離散的な点の集合として表現される。線分は、2端点(ｘ_１,ｙ_１),(ｘ_２,ｙ_２) の座標で定義される。この線分を描画するために直線の方程式を用いる方法もある。

ｙ＝ (x-x₁)*(y₂-y₁)/(x₂-x₁) + y₁　 　　

この式は、2端点間にあるすべての点に対するx, y座標を求めるために使われ、xをからまで動かしてyの値を求める。ただし、x, yは整数値である。なお、走 査線の順序で線を描画する処理は走査変換（スキャンコンバージョン: scan conversion）とよばれる。また、各走査線ごとに直線の方程式を解くのではなく、1つ前の走査線での交点に増分を加える増分法が一般に用いられる。

(2)　ブレセンハム(Bresenham)のアルゴリズム

　線の最良な近似は、真の直線から最短距離にあるような画素を並べたものです。真の直線とそのすぐ上およびすぐ下の画素との距離をs_i，t_iとし、d_i=si-t_iとすると、d_iの符合で真の曲線のどちらの画素を選択するかが決められ、このは簡単な加算のみで求められる。このように、加算のみで処理できる簡単方法をブレセンハムのアルゴリズムという。 効率よい計算のため整数演算で実現できるように改良されている。なお、任意の方向の直線の場合にも対応できるには場合分けが必要である。

始点（x0, y0）、終点（x1, y1）の線分を考える。なお、 説明を簡単にするため、線分が第１オクタントの場合（dx>dy>0）に限る。ただし、dx=x1-x0, dy=y1-y0. 整数表現の直線とｙの真の直線のｙとの差の誤差ｅとすると、ｘが１増分に対し、ｙを１増分させない場合の誤差は

となる。なお初期では誤差eは0である。これは次のアルゴリズムで記述できる。

1. 誤差eを0に初期化し、画素（x0、y0）を描画
2. x0＋１からx1まで、ｘを１つずつ増分させて以下を繰り返す。

1. if e+dy/dx>=0.5 なら y = y+1, e = e+ dy/dx ?1

実数演算をさけるため、誤差の式から0.5を減じ、2ｄｘを乗じた新しい誤差ｄを用いると、

1. 誤差ｄの初期値を計算し、画素（x0、y0）を描画

d = 2dy-dx

2. x1＋１からx2まで、ｘを１つずつ増分させて以下を繰り返す。

1. if d>=0 なら y = y+1, d = d+ 2(dy-dx)

始点（x0, y0）、終点（x1, y1）の線分を描画するプログラムは次のようである。なお、 説明を簡単にするため、第１オクタントの場合（dx>dy>0）に限ってある。

int x,y=y0; dx = 2*(x1-x0), dy = 2*(y1-y0) int dydx = dy - dx, d = dy - dx/2; 　 for(x=x0; x<=x1; x++){ draw_pixel(x,y); if(d<0) d+= dy; else {y+=1; d += dydx;}

関数 scanX を BresenDraw から呼ぶ例を以下に示している。

上記は、基本的にはｘ方向に一つづつ進むが、変数epsが正になるときはｙも一つ進むアルゴリズムである。このプログラム前記アルゴリズムを変更（誤差の初期値）している。他のケースの場合の含めて動作するためには、線分の傾きに応じて場合分けが必要であるので、実際のプログラムを参照のこと。

３）プログラム使用法

マウスにより２端点を指定するものと、予め設定した２点を結ぶ簡易版が容易されているから、簡易版から実験をする。マウスでクリックした点は黄色の小円で表示され、２点目をクリックした際線分が表示される。さらに画面内のどこかをクリックすると画面がクリアーされ、再度線分を指定できる。

2. コッホ曲線

　山、雲、木等も自然物を表現するにはフラクタルが有用です。フラクタルと いう言葉は、マンデルブロ(Mandelbrot)による造語です。フラクタルは、不規則な形状、自己相似性をもつ形態を表現できます。これにより、自然界の物を模擬し、自然の情景を描写することができます。例として、コッホの曲線があり、相似な大小の形状が組み合わされています。

コッホ曲線は、同じ処理を繰り返すことによって作成しているため、図の一部分を拡大しても同じ図形が現れる。直線を細かく描くことによって、曲線のように見えるのでコッホ曲線とよばれる。海岸線や雲も同じような図形である。

図5.1 コッホの曲線の分割過程

図5.２ コッホの曲線（レベル５の場合）

1. 直線を引く。
2. 直線を3等分する（図（ｂ）参照）。
3. 3等分した長さを一辺とする三角形を作成する。
4. 1つの辺に対して、同じように3等分して、この処理を繰り返す。

（a）x0、y0は、線分の開始位置を示し、angleは、線分の角度を表す。

（b） 1本の線分の長さ（leng）を計算する。

（c） コッホ曲線を1本作成するメソッド（draw）を呼び出す。

（d） ｎ回のコッホ曲線を作成するメソッドを呼び出す。線分の角度を0度、60度、―120度、60度回転させて直線を引く。

（e） 次の点のｘ、ｙ座標は次式で計算する。

ｘ= leng・cos（60°）

y = leng･sin(60°)

(f) 0度、60度、-120度、60度回転させてdrawを再帰的に呼び出す。

ここでの例は、クラスKochCurvを使う方法とした。このクラスに描き初めの座標(x0,y0)、角度(angle)、長さ(leng)、および繰り返しレベル ｎを指定するすることによる再帰的描画方法とする。

1) コッホ曲線のクラス；曲線の初期値設定および再帰的描画

class KochCurv{ double x0,y0, angle; // (x0,y0);端点座標、angle；角度 KochCurv() { } // コンストラクター 　 public void draw(int I, double leng, Graphics gr) { If ( i == 0) { double rd = 3.1415927/180.; double x = leng * Math.cos(rd * angle) + x0 ; double y = -leng * Math.sin(rd * angle) + y0; gr.drawLine((int)x0,(int)y0,(int)x, (int)y); // 線分を描画 x0 = x; y0 = y; } // 終点を次の線分の始点に置き換え else { draw(i ? 1, leng, gr); angle += 60.; draw(i ? 1, leng, gr); angle -= 120.; draw(i ? 1, leng, gr); angle += 60.;; draw(i ? 1, leng, gr); } } 　 public void setPoint(double lpx, double lpy) { // 始点を設定 x0= lpx ; y0 = lpy ; } public void setangle(double a) { // 角度の初期値設定 angle = a; } }

2) コッホ曲線の描画関数:

public void paint(Graphics g) { KochCurv koch = new KochCurv(); // ｵﾌﾞｼﾞｪｸﾄの生成 koch.setPoint(30.0, 140.); // 始点の座標指定 koch.setangle(0.0); //角度の初期値設定 double leng = 400 * Math.pow(0.33333, n); koch.draw(n, leng, g); // コッホ曲線描画 }

このプラグラムは再帰呼び出しの回数をHTMLによって指定できるが、下記のようにvalueの値でしていする。なお、デフォルトは５回である。

5. ３ ]一価関数の隠線消去

この隠線消去はスクリーン空間で行われる。基本的な考え方は、ｘ、ｙ、またはｚの一定値による幾つかの平行平面による曲面を考える。すなわち、幾つかの曲線の集合で表現できる。これらの切断曲線をスクリーンに投影し、２次元スクリーン上で隠線消去を行なう。その際、視点に近い断面上の曲線から順に描画する。

いま、ｘ、ｙ平面がスクリーンに対応し奥行きがｚ軸となる座標系を考える。この方法は投影後のスクリーン座標において隠線消去を行なう方法である。一価関数で表現される曲面がこの隠線消去に適している。一価関数とは、ｚ＝ｆ（ｘ、ｙ）のように与えられたｘ、ｙ座標に対しｚは１個しか価が存在しない関数である。ここでは、ｙ＝ｆ（ｘ、ｚ）の関数を考え、ｚ = zi （I=0,1,…n）の際の曲線を描く。ここで、視点に近い順に描画する。その際描画した曲線が存在した最大値と最小値を各ｘ座標（スクリーン座標）について記憶する。次の層の曲線を描く際記憶している最大値と最小値の範囲外なら描画し、そうでないなら描画しない。この操作を繰り返す。

1. 最大・最小値を記憶するバッファを初期化する。
2. 曲線を手前から順に生成（ｚ＝ｆ（ｘ、ｙ））し、

点P(x, y,z)を透視投影しスクリーン座標p’(x’,y’)を算出する。

3. 最大・最小関数から、可視判定を行なう。可視なら点 p’ 描画し、最大・最小関数を更新する。

3次元座標の透視変換を行なうクラスTrans、注視点、視点を設定し、変換マトリックスの係数を計算した後に、各頂点について座標変換（または投影）を行なう。座標変換の場合は３次元座標（３次元の実数のクラスPoint3）、投影の場合は２次元（２次元の整数クラスPoint）が戻る。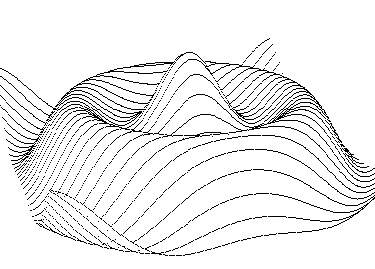

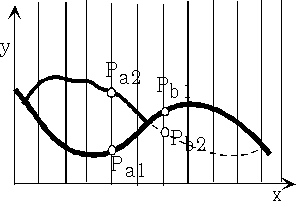
なお、 視点は極座標（R、θ、Φ）で与える。マウスをドラッグして動かすと、視点が変化できるようにする。この際、マウスを左右するとθ、上下させるとΦが変化するものとする。

図５．３ 関数の隠線消去の例 図５．４ 最大値を利用した隠線消去

曲面を上方から眺めている場合を考える。図５．４に示すように、既にＰａ1、Ｐｂ１を通過する曲線が描かれているとき（その際各画素でのｙの値は記憶）、Ｐ_a2,P_b2を通過する曲線を描く場合、点Ｐ_a2においては記憶されているｙの値（すなわちＰ_ａ1のｙ）より大きので可視、またＰ_ｂ2においては記憶されているｙの値より小さいから不可視と判定される。

class Trans { Point3 ptViewRef = new Point3(0, 0, 0); // 注視点の3次元座標 double theta, phi, R; // 視点位置（Ｒ、θ、Φ） double cos_theta=1., cos_phi=1., sin_theta=0., sin_phi=0.; Trans() { } 　 public void setVRpnt( double x, double y, double z) { ptViewRef = new Point3(x,y,z); } // 注視点の設定 public void setview(double r, double the, double ph) { theta=the; phi=ph; R=r; } // 視点の設定 public void preper() { // 変換マトリックスの係数計算 double d2r= Math.PI/180.; cos_theta =Math.cos(theta*d2r); sin_theta = Math.sin(theta*d2r); cos_phi = Math.cos(phi*d2r); sin_phi = Math.sin(phi*d2r); } 　 public Point3 tranfrm(Point3 point) { // 透視変換(3次元à 3次元） Point3 p1 = new Point3(); Point3 p2 = new Point3(); // 平行移動 p1.x = point.x ? ptViewRef.x; p1.y = point.y ? ptViewRef.y; p1.z = point.z ? ptViewRef.z; // 座標回転 double xy = cos_theta*p1.x+sin_theta*p1.y; p2.z =(R-cos_phi*xy-sin_phi*p1.z)/R; p2.x = cos_theta*p1.y-sin_theta*p1.x; p2.y = cos_phi * p1.z ? sin_phi * xy; return p2; } public Point project (Point3 point) { // 投影（3次元à 2次元） Point3 p1= tranfrm(point); Return new Point((int)(p1.x/p1.z), (int)(p1.y/p1.z)); } }

透視投影の式は資料[1]の2.6を参照のこと。

実数の３次元座標を記憶するクラスPoint3 を準備する。

3) 曲線を描画する関数

ここで、（x_origin、y_origin）はスクリーンの中心座標で, width, height はスクリーンサイズである。上のプログラムは視線とＺ軸とのなす角が９０度以内のときのみうまくいくもので、他の方向から見る場合には、描画する曲線の順を変更する必要がある（例えば、ｙループの中にｚループとする）。描画する点のスクリーン座標（px,py）を考えると、py < ymin[px] またはpy > ymax[px] ならその点は可視であり、ymin[px] またはymax[px]を更新する。

4) 曲面関数生成

ここでの関数FuncHatの例は z = z₀(cos(sgrt(x²+y²)) + cos(3sqrt(x²+y²))) を用いた。戻り値は３次元座標を表現できるPoint3クラスである。

public Point3 FuncHat(int x, int y) { // Function z = F(x,y) double rd= Math.PI/180; 　 double r = Math.sqrt(x*x+y*y)*rd; double z = 30.*(Math.cos(r) + Math.cos(3.*r)); return new Point3(x, y, z); }

ワイヤーフレーム表示とは、隠線消去を行なわないで表示する方法である。ここでは簡単のため凸多面体の代表的な立方体を対象とする。 視点は極座標（R、θ、Φ）で与える。マウスをドラッグして動かすと、視点が変化できるようにする。この際、マウスを左右するとθ、上下させるとΦが変化するものとする。

基本的には、次の手順からなる。

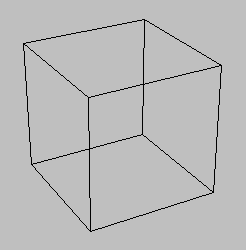
立方体の場合、８頂点と６面からなる。これを記憶するため、頂点の3次元座標を記憶するクラス Point3 （５．３参照）と、面を記憶するクラス Plane を準備する。また、座標変換のためのクラスTrans （5.3参照）も利用する。

多面体は頂点および面に番号を付けし、各頂点の3次元座標はpoint[ ] (クラス Point3）に、面はその構成頂点を face[ ] (クラス Plane)に記憶する（データ構造は資料[1]参照）。描画は面単位に行なう（クラス Plane のメソッドdrawを利用）。この方法では、辺は２つの面の稜線であるため辺は２度描きされている。

ここで使用している配列とクラスとの関係は下記のようである。

1) 立方体の描画関数

2) 立方体生成の関数；

面（多角形）の構成番号を記憶し、描画する。

class Plane { public int set[ ]; // 面の構成頂点の配列 public int npoint=0; // 面の頂点数 Plane() { set = new int[4]; } // 面の構成頂点番号の配列の確保 public void add(int k) { // 頂点番号の追加 set[npoint] = k; npoint ++; } 　 public void draw(Graphics g, int x_origin,int y_origin,Point point[]) { for (int i = 0; i < npoint; i++) { int ii = i+1; if(ii==npoint) ii=0; g.drawLine(point[set[I]].x+x_origin, y_origin-point[set[i]].y, // 各辺の描画 point[set[ii]].x+x_origin, y_origin ? point[set[ii]].y); } } }

1) 下記ディレクトリからJavaソースおよびHTMLファイルをコピーして練習して下さい。

BresenS.javaはBresen.javaのマウス部分が無いものである。JDK.1.１とJDK.1.0に対応するため、JDK.1.１用のものはJDK.1.0部分はコメントとしている。JDK.1.0対応のものはコンパイル時に警告が出るが、実行可能なので警告は無視して下さい。

練習問題を行なうに当たっては、マウスの機能の有無、背景や線の色の変更、画面サイズの変更、見る方向変更などを試みて、自分なりのプログラムに修正して下さい。

• Bresenhamの直線描画： HTMLファイルで描画する２端点の座標を指定できるように変更してみる。

• コッホ曲線の描画； マウスで画面をクリックするごと複雑な図形になるようにする。すなわちレベルｎをマウスクリックで１づつ増加するように変更
• 一価関数曲面の表示： 関数を変更する。
• 多面体のワイヤーフレーム表示； 立方体のデータを直方体に変更する。

また、練習課題に関する最新情報は ~knisi1482/index.html をブラウザーで起動して参考にして下さい。

2) 本科目に関する情報（課題等）は、下記ＵＲＬを参照して下さい。