  
|
  
|
|
5.9 フラクタル
山、雲、木等も自然物を表現するにはフラクタルが有用です。フラクタルという言葉は、マンデルブロ(Mandelbrot)による造語です。フラクタルは、不規則な形状、自己相似性をもつ形態を表現できます。これにより、自然界の物を模擬し、自然の情景を描写することができます。図5.35はコッホの曲線を示します。相似な大小の形状が組み合わされています。 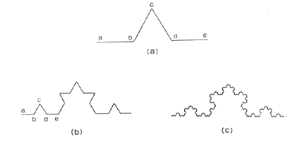
図5.35: コッホの曲線
図(a)に示すように、辺b c上にb c dと相似で1/3に縮小したものを生成します。同様に、a b, d eにも生成すると図(b)となります。次々にこの処理を繰り返すと、図(c)が得られます。この場合、辺の長さはn回目には
(1) フラクタル次元
一般にはユークリッド幾何学における次元は整数です。しかし、フラクタル次元は非整数です。例えば海岸のフラクタル次元は約1.2です。非常に入りくんだ海岸ではさらに大きくなります。このようにフラクタルの特徴を定量的に表す量がフラクタル次元です。自己相似性のある図形において、図形を
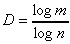 (5.21) (5.21)
コッホの曲線の場合、
(2) 中点変位法
少ないデータの入力で複雑な3次元形状を生成できることが望ましい。この一つの方法としてフラクタル理論を用いる方法があります。まず簡単なフラクタル図形の生成を紹介します。有限個の線分からなる2次元図形を、各線分ごとに再帰的に分割を繰り返して非常に細かい線分からなる図形を得ることができます。これは次の手順で処理します(図5.36参照)。
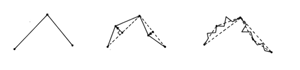
図5.36: 中点変位法によるフラクタル
(a) 概形図形を与える(図(a)参照)。
(b) 各線分の中点を求めて、その位置からその線分の法線方向に乱数で振って新しい点とする。
(c) 乱数の振幅(分散に相当)を
必要な精度(線分長)となるまで (2)-(b),(2)-(c)の処理を繰り返す(図(c)参照)。 ここで、hは形状のぎざぎざ度を制御するパラメータである。

図5.37: フラクタルによる海岸線の生成(四国の例)
図5.37は、中点変位法により生成した四国である。(a)が原型で、(b)が生成後です。次に、3次元物体の例として山岳の表現を考えてみましょう。山岳を生成する手順は次のような手順です。
(a) 山の概形を与えるため、メッシュでの標高値を与える。すなわち、標高値のデータ構造を2次元配列で作る。
(b) メッシュを構成する4辺の中点において、新たな標高を次式によって求める(図5.38参照)。
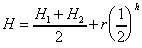 (5.22) (5.22)
第2項がフラクタル変位量です。rは乱数で、hは前出の複雑さを示す定数です。このhにより減衰の割合を加減できます。
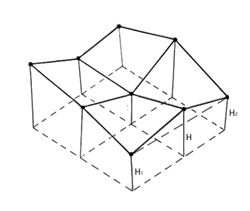
図5.38: 中点変位法による図形生成
フラクタル量は、分割レベルに比例して小さくなります。
左図は中点変位法による山じゃけん。
上の例は4辺形で1つの面を構成したが、3角形を基本とし、3角形の3辺の中点を変動させ、新たな4つの3角形を発生する方法もあります。
|
 前のページへ 前のページへ
| 次のページへ
|