  
|
  
|
本章では、図形の描画の考え方、座標系、座標変換について説明する。 | |
| 2.1 図形の描画法
2次元図形を構成する基本要素としては、点,線分,多角形,円,平面,曲線などがある。たとえば、点はx, y座標で定義され、線分は2端点の座標で定義される。また、多角形は頂点のつながり(または線分のつながり)として定義される。これらの図形は、フレームメモリ(frame memory)上に描くことによりスクリーンに表示される。 (1) 直線の描画
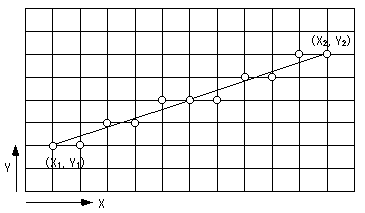 図2.1: 直線の描画
ラスタスキャン方式のディスプレイでは、直線は離散的な点の集合として表現される。線分は、2端点 (
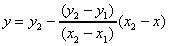 (2.1) (2.1)
この式は、2端点間にあるすべての点に対するx, y座標を求めるために使われ、xを (2) ブレセンハム(Bresenham)のアルゴリズム
直線の最良な近似は、真の直線から最短距離にあるような画素を並べたものです。真の直線とそのすぐ上およびすぐ下の画素との距離を (3) 円の描画法 円を描くためには、次の式がよく用いられます。角度tを増分することによって、円上の座標(x, y)を順に計算することができる。 x=rcos(t)y=rsin(t) この実数計算は、誤差の問題や計算時間がかかることから、最近は整数計算による方法を用いることによって、画素を並べた近似円を描いています。この整数計算による円の描画アルゴリズムはいくつか提案されている。 (4) ペイント(paint) 領域の塗りつぶしとは、与えられた領域あるいは範囲を彩色する操作である。これには大別して2つの方法がある。1つは、種とよばれる最初の画素を与え、この種から出発して、種を囲む画素について、境界内かどうかを調べ、領域内のすべての画素を検査し終えるまでくり返される。また、第2の方法は、走査線を上から下に移動させ、図形の境界と走査線との交点を求め、交点間を塗りつぶす方法である。この操作を走査変換とよぶ。 | |
 前のページへ 前のページへ
| 次のページへ
|