3.4 曲面の表現形式およびその表示
曲面(パッチとも言う)の表現法としては、陰関数表現とパラメトリック表現がある。前者としては、例えば2次曲面は次のように表現される。
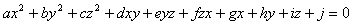 (3.1) (3.1)
いずれにしても、fをx, y, zの関数としたとき、一般に f(x, y, z) = 0 の形式で表現されるものを陰関数という。一方、後者としては、u, vをパラメータとして次式のように表現される。
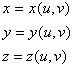 (3.2) (3.2)
パラメトリック曲面としては、種々の表現形式がある。双3次曲面、ベツィエ曲面、有理ベツィエ曲面、B-スプライン曲面、NURBS(Non-uniform Rational B-spline Surface)、ベータスプライン曲面、クーンズ曲面、グレゴリ曲面などである。最近ではNURBSを主としたCADシステムが増加している傾向にある。
曲面をどの表現形式で入力するかは、入力の容易性に大きく影響する。また、形状データの他システムとの互換性も考慮する必要がある。操作性のよい表現形式とレンダリングに都合がよい形式は必ずしも一致しないので表現形式の変換機能を有したシステムもある。
まず曲線について説明し、次に曲面について説明する。
(1) ベツィエ曲線
ルノー社のベツィエ(B'ezier、ベジエと呼ぶこともある)は、制御点を与えることによって、描かれる曲線を表す形式を提案した。この方法は、対話式に制御点を与えることにより容易に曲線の形状を推測できる特徴がある。
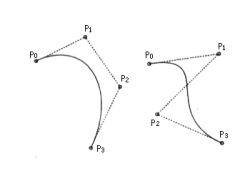
図3.5:3次ベツィエ曲線
それでは、Javaで実際に体験してみましょう。
図3.5は、4点を与えて得られたB'ezier曲線である。この曲線は3次の多項式となる。n次のB'ezier曲線は、パラメータuを用いて次式によって表現される。
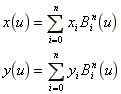 (3.3) (3.3)
ここで(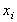 , ,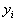 )は制御点の座標で、B は次式で示されるn 次の関数で、バーンシュタイン(Bernstein)の基底関数と呼ばれ次式で表される。 )は制御点の座標で、B は次式で示されるn 次の関数で、バーンシュタイン(Bernstein)の基底関数と呼ばれ次式で表される。
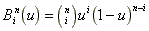 (3.4) (3.4)
具体的な例を示すと、n=3なら
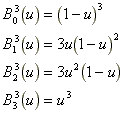 (3.5) (3.5)
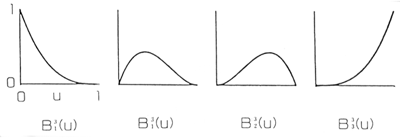
図3.6:3次の混合関数
となる。図3.6にn=3に対するBを示す。Bは混合関数ともいわれる。すなわち、これらの関数は各制御点がuの値によって曲線に及ぼす影響を表している。ここで、uは0から1まで変化し、0の時は始点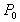 、1の時は、終点 、1の時は、終点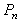 と一致する。 と一致する。
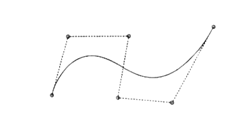
図3.7:高次ベツィエ曲線
図3.7は高次(n=5)のベツィエ曲線の例を示している。2つのベツィエ曲線を接続するには次の条件を満足させる必要がある。すなわち、一方の曲線の端点と他方の曲線の端点が一致するのはもちろん、接線まで連続にするには、接続点の頂点の前後の2頂点と接続点が同一直線上に存在する必要がある。
ベツィエ曲線の特徴は次のようである。
・ 必ず2つの端点、すなわち、始点と終点を通過する。
・ 始点、終点における接線ベクトルの向きは、それぞれベクトル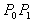 、ベクトル 、ベクトル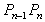 の方向に一致する。 の方向に一致する。
・ 制御点を囲む最小の凸多角形を凸包と呼ぶが、ベツィエ曲線の凸包に対して曲線は必ず内側に存在する。
(2) B-スプライン曲線
ベツィエ曲線は、曲線同士を接続する際、その連続性を保証するのが困難である。これを解決するのがB-スプラインである。B-スプラインは次式で表現される。
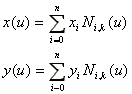 (3.6) (3.6)
ここで、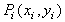 は制御点で、Nはuの多項式で表現される混合関数、すなわちB-スプライン関数である。kはB-スプライン関数の階数(order)で、k-1が次数(degree)である。k-1次のB-スプライン混合関数は次のように帰納的に定義される。 は制御点で、Nはuの多項式で表現される混合関数、すなわちB-スプライン関数である。kはB-スプライン関数の階数(order)で、k-1が次数(degree)である。k-1次のB-スプライン混合関数は次のように帰納的に定義される。
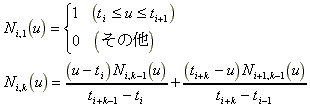 (3.7) (3.7)
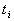 は結節点(knot)と呼ばれる。一般には0,1,2,..n-k+2のように等間隔にとられる。階数4、次数3の場合のB-スプライン関数は次式となる。 は結節点(knot)と呼ばれる。一般には0,1,2,..n-k+2のように等間隔にとられる。階数4、次数3の場合のB-スプライン関数は次式となる。
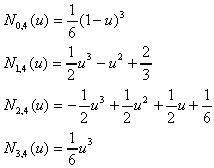 (3.8) (3.8)
ベツィエ曲線の場合、uは0から1であったが、B-スプラインの場合、0からn-k+2の範囲で変化させる。図3.8にB-スプライン曲線の例を示す。ここで、図3.7と同じ制御点を例に、次数を変化させた場合の曲線を示している。
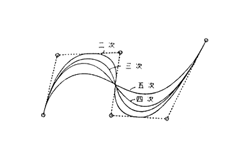
図3.8:B-スプライン曲線
図でわかるように、制御点の数と(次数+1)が一致するときは、ベツィエ曲線と同じ曲線となる。 また、次数が増加するに従って、曲線が張ったようになる性質がある。既に述べたベツィエ曲線に比べて、B-スプラインには次の特徴がある。
・ 曲線の接続点で連続性が保証されている。
・ 形状制御を局所的に行うことができる。
(3) ベツィエ曲面
ベツィエ曲線同士の直積によって3次元曲面を記述することができる。n×m次B'ezier曲面は次式で表される。
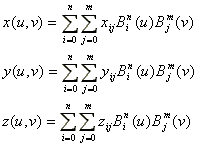 (3.9) (3.9)
ここで、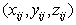 は制御点の座標であり、制御点は網目状に配列された(n+1)×(m+1)の制御点をもつ。図3.9に3次のベツィエ曲面を示す。隣接した制御点は網目(制御ネットと呼ばれる、図では点線で示す)を示すため、直線で結ばれている。図(a)のように(3次の例)、線画で曲面を表示する際は、u,v2組の曲線を描くことで示される。1組はパラメータvを一定に保ち、uを0から1まで変化させ、もう1組は、パラメータuを一定に保ち、vを0から1まで変化させる。これらの曲線は前述のベツィエ曲線である。図(b)は陰影表示したもので((a)とは異なる制御点)、制御ネットを重ねてある。また、球は制御点の位置を示しているが、隠面消去により、曲面に隠される球は表示されていない。曲面上で白っぽくなっている部分があるが、これはハイライトとよばれ鏡面反射によるものである。 は制御点の座標であり、制御点は網目状に配列された(n+1)×(m+1)の制御点をもつ。図3.9に3次のベツィエ曲面を示す。隣接した制御点は網目(制御ネットと呼ばれる、図では点線で示す)を示すため、直線で結ばれている。図(a)のように(3次の例)、線画で曲面を表示する際は、u,v2組の曲線を描くことで示される。1組はパラメータvを一定に保ち、uを0から1まで変化させ、もう1組は、パラメータuを一定に保ち、vを0から1まで変化させる。これらの曲線は前述のベツィエ曲線である。図(b)は陰影表示したもので((a)とは異なる制御点)、制御ネットを重ねてある。また、球は制御点の位置を示しているが、隠面消去により、曲面に隠される球は表示されていない。曲面上で白っぽくなっている部分があるが、これはハイライトとよばれ鏡面反射によるものである。
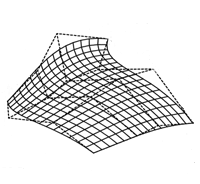 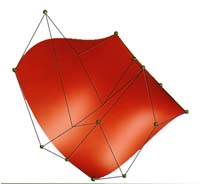
(a) (b)
図3.9:ベツィエ曲面
(4) B-スプライン曲面
B-スプラインは、ベツィエ曲面と同じように、直積によって曲面を記述できる。
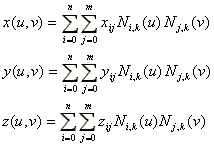 (3.10) (3.10)

図3.10:Bスプライン曲面
図3.10にB-スプライン曲面の例を示す。なお、制御ネットは点線で示している。
| 





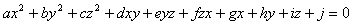 (3.1)
(3.1)
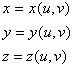 (3.2)
(3.2)
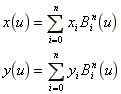 (3.3)
(3.3)
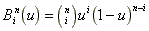 (3.4)
(3.4)
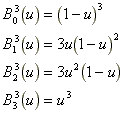 (3.5)
(3.5)


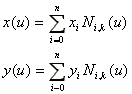 (3.6)
(3.6)
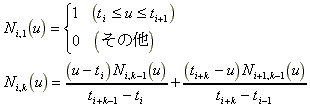 (3.7)
(3.7)
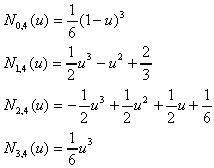 (3.8)
(3.8)

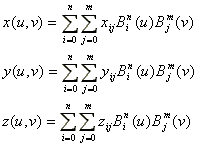 (3.9)
(3.9)

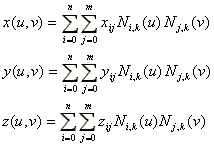 (3.10)
(3.10)
 前のページへ
前のページへ
