スムーズ・シェーディングには次の2つの方法があります。
(1) 輝度の補間
この方法は、グロー(Gouraud)のスムーズ・シェーディングと呼ばれます。曲面を多角形に分割し、各多角形の各頂点での輝度を求めておき、まず、多角形と走査線との交点(図5.20の点L,R)での輝度を 線形補間によって求め、
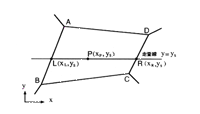
図5.20: 輝度の補間によるスムーズシェーディング
次に走査線上の各画素(例えば、図のP)での輝度を線形補間により求めます。すなわち、多角形(例えば頂点 A, B, C,Dよりなる多角形)内部における点Pの輝度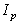 は次式によって求められます。
は次式によって求められます。
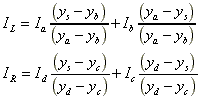 (5.11)
(5.11)
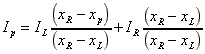 (5.12)
(5.12)
ここで、
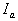 ,
,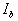 ,
,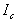 ,
,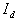 ,
,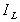 および
および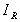 はそれぞれ点A,B,C,D,LおよびRにおける輝度です。
はそれぞれ点A,B,C,D,LおよびRにおける輝度です。
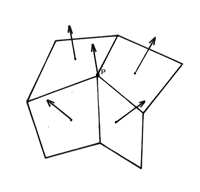
図5.21: 法線ベクトルの計算
なお、多角形の頂点における法線ベクトルは、その頂点(図5.21の点P)を含む多角形の法線ベクトルの平均値を用います。この方法では、輝度のみ補間することから、ハイライトの計算が正しくできない欠点があります。
たとえば、多角形の内部にハイライトがある場合、頂点のみで輝度を求めた場合いずれの頂点もハイライトは求まっていないのでそれらから補間したのでは、当然ハイライトは生じません。また、補間は線形補間であるため、多角形同士の境界部ではスムーズに明るさが変化するのではなく、折れ線的に変化します。
すなわち、マッファバンド効果は減少するが、完全にスムーズになるとは限りません。
(2) 法線ベクトルの補間
この方法は、フォン(Phong)のスムーズ・シェーディングと呼ばれます。
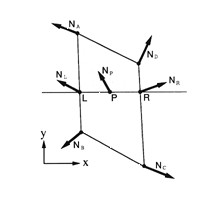
図5.22: 法線ベクトルの補間によるスムーズシェーディング
曲面を多角形に分割し、各多角形の各頂点での法線ベクトルを求めておき (図5.21参照)、まず、多角形と走査線との交点 (図5.22の点L,R)での法線ベクトルを線形補間により求め、次に走査線上の各画素(例えば、図のP)での法線ベクトルを線形補間により求めます。
すなわち、多角形内の点Pでの法線ベクトル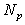 は、式(1)と同様な方法によって求まります。
は、式(1)と同様な方法によって求まります。
ここで、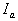 ,
,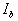 ,
,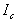 ,
,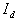 ,
,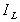 ,
,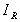 を
を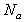 ,
,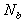 ,
,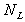 ,
,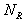 で置き換えればればよいです。
で置き換えればればよいです。
補間により得られた法線ベクトルと光源の位置から点Pにおける輝度を計算することができます。この方法は、前述の方法と比べてより精度のよい方法であり、ハイライトが計算できます。
図5.23にコンスタントシェーディングと スムーズシェ−ディングの比較を示します。

(a)constant shading


(b)Gouraud shading (c)Phong shading
図5.23: スムーズシェーディングの比較例
なお、図(b)はグローシェーディングで、図(c)は多角形近似しない方法での隠面処理後 フォンシェーディングを施したものです。





