コンピュータグラフィックス論 課題(2004年度)
下記のプログラミング課題において4問中少なくとも3問を提出せよ。
プログラミング課題
インタラクティブ性のあるプログラムが理想であり、
それを遠隔地でも評価するにはJavaで作成すると効果的であるので、可能な人はできるだけJavaを試みて下さい(この場合画像サイズは300x300以下でもよい)。
C言語とOpenGLを用いて表示する方法でもよい。
この際、出力例がカラー画像の場合、それを評価して欲しい人は、自分のホームページに画像を置いて見れるようにしてもよい。
課題1 フラクタル(自己相似性)の考え方を用いて、線画によって樹木を描画するプログラムを作成せよ(教科書p.88、p.101参照)。
- 海岸線、雲や煙の形状、植物などの形は、全体の形と部分の形がよく似ているという特徴がある。このような特徴をもつ図形をフラクタルという。
- 図1はフラクタルによる樹木生成の単純な生成プロセスを表している。そのアルゴリズムは次のようになる。
- 初期値として幹(図1 太線)と枝(図1 細い線)に相当する線の始点と長さを与える。
- 枝は先端で3方向に分岐し、幹はまっすぐ成長する。分岐した枝には、それぞれがまた次の幹と枝を持つ。
- 2.の操作をn回繰り返す。
- このアルゴリズムで、分岐数、枝分かれの仕方、枝分かれの角度、長さの割合といったパラメータを変えれば、図2のようにさまざまなバリエーションの樹木が得られる。さらに、日照や風などの枝の成長に影響するパラメータを加えれば、より本物の樹木らしい図形が得られる。作成するプログラムは、このようにインタラクティブにパラメータを変更でき、様々な樹木を描画できるものが望ましい。
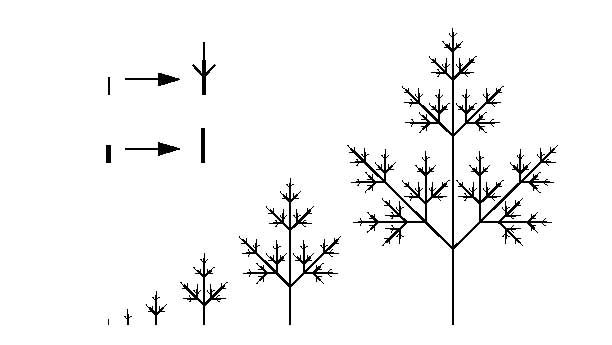
図1 フラクタルによる樹木の生成(© Prusinkiewicz)
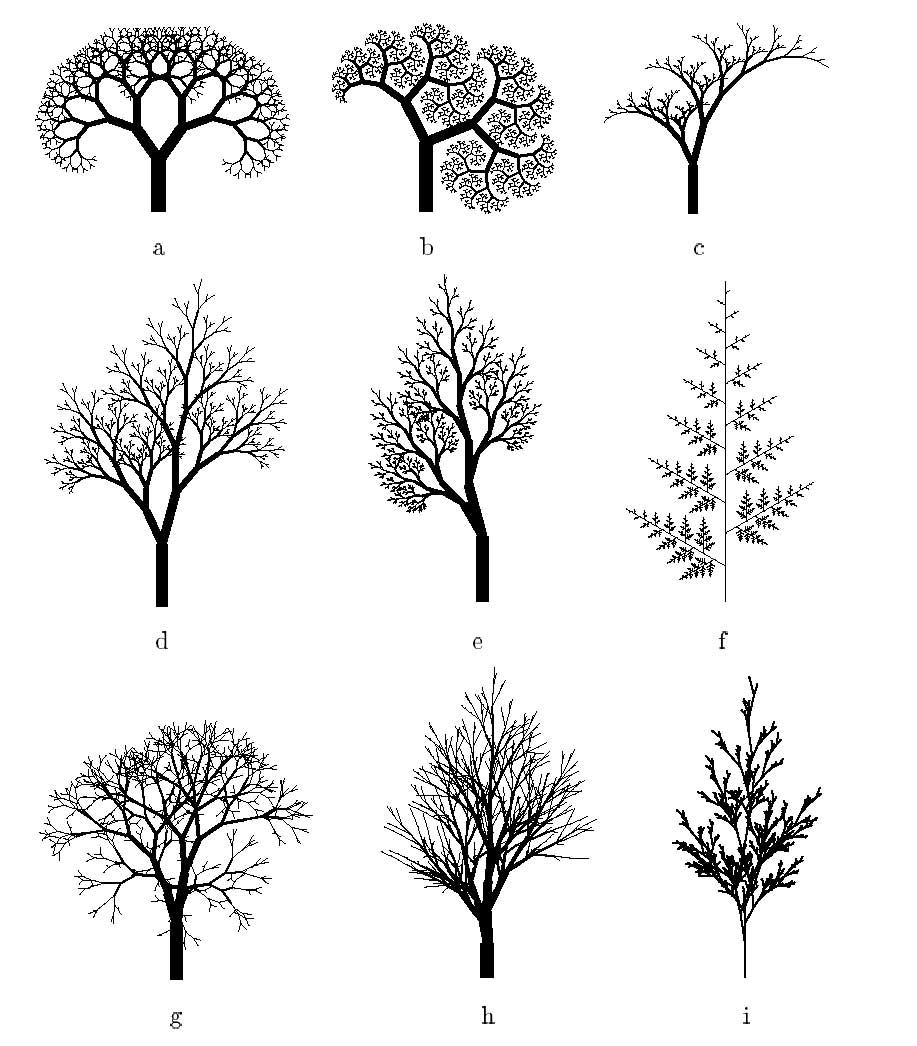
図2 様々な生成パラメータを変化させた時の生成される樹木のバリエーション(© Prusinkiewicz)
課題2 2次元空間でテクスチャマッピングを行うプログラムを作成せよ(教科書p.165参照)。
- 最初に画像データをプログラムで読み込み色データの配列を記憶する。画像読み込みができないときには、縞模様やチェック模様などの簡単なものをプログラム内で作成してもかまわない。
- 次に4点を指定し、それを囲む4角形内部にテクスチャの頂点と、指定した4角形の頂点を一致させ4角形内部も描画する。このとき4角形がねじれる場合は考慮しなくてよい。
- 指定4角形内部の描画のためには、テクスチャのピクセルに最も近い座標の色をコピーする最近点サンプリング、またはテクスチャのピクセルに最も近い点の上下左右にあるピクセルの加重平均を計算する線形フィルタリングを用いよ。
- 指定4角形が元のテクスチャよりかなり小さくなる場合には、あらかじめ元のテクスチャ(64×64)の縮小された解像度の画像(32×32、16×16…)を作成しておくと効率的に描画を行うことができる。(この考え方をミップマップという。)
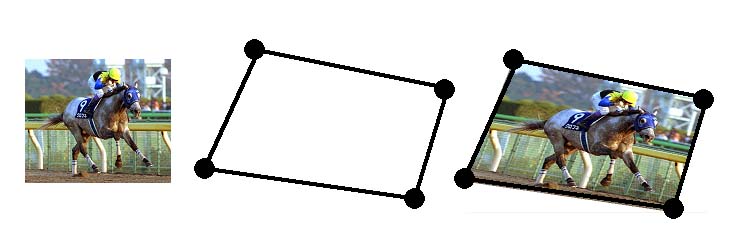
図3 テクスチャマッピング 左:用意した元テクスチャ 真中:4点を指定 右:指定した4点による4角形にテクスチャをマッピング
課題3 凸多面体を任意の位置から見た透視投影で描画せよ。
- 3次元上の点の透視投影は参考文献[2]を参照
- 下図のようにワイヤーフレーム表示せよ。
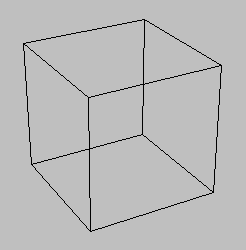
- 視点から見た面の表裏を利用して、隠線消去した図を描画せよ。
課題4 課題3の凸多面体をレイトレーシング法で描画せよ。
- 多角形は3角形に分割し、3角形とレイの交点計算(教科書p。141参照)を利用して描画せよ。
- 陰影は平行光線とし、各面の明るさを計算せよ。
JavaやX-windowの使用方法を勉強する時間のない場合は、次の方法でもよい。
すなわち、スクリーンを想定した配列を準備し、それに輝度情報を書き込み、準備したツールで可視化する。
画像サイズは500x400程度とする。ただし、プログラムリストと結果のハードコピー(PostScript形式にしプリント)を提出すること。
この際、画像をセーブすることが必要になるが、保存の画像形式およびそのプログラムは資料を参考にして下さい。
注:プログラミングが困難な学生は相談に応じてレポート課題を提出する方法も考慮します(メイルしてください)。
参考文献(図書)
- [1] 配布資料; 中前、西田 「3次元コンピュータグラフィックス」昭晃堂
(p.63 -109 )
- [2] /~nis/CG/cgtxt/cg2/cg026.htm#cg26
- [3] 「技術編CG標準テキストブック」、 CGARTS(画像情報教育振興協会)
- 参照URL
- 締切: 8月18日(水曜)
結果は各自のホームページに置くか、印字して事務室に提出、あるいはメイルに添付して下さい。
連絡先:email: nis@is.s.u-tokyo.ac.jp
電話: 内線24106 (西田研究室):
/~nis/




