インタラクテイブ性のあるプログラムが理想であり、それを遠隔地でも評価するにはJavaで作成すると効果的であるの
で、可能な人はできるだけJavaを試みなさい(この場合画像サイズは300x300以下でもよい)。 X-WindowあるいはOpenGLを用い
てスクリーン上に表示する方法でもよい。この際、出力例がカラー画像の場合、それを評価して欲しい人は、自分のホ
ームページに画像を置いて見れるようにしても良い。
課題1 Bezier曲面を表示するプログラムを作成せよ。
- 任意の位置から見た曲面を線画で表示すること。
- 曲面は等パラメータ曲線を表示するものとし、曲線上の座標の計算はde Castejouの方法を用いる.
- 曲面の制御点から分割法により等パラメータ曲線の制御点を得て、それから曲線上の点列を結んで描画する(資料[1]参照)。
- 制御点を投影し、投影した制御点をもとに曲線を描画する(3次元上の曲線上の各点を投影するのが正確)。
- 視点をR、θ、Φで与えた場合の透視投影の式は下記を参照して下さい。
/~nis/CG/cgtxt/cg2/cg026.htm
- 曲面の場合、隠面消去は容易ではないが、特殊な条件の際は簡単な方法が用いることができる。すなわち、Bezier曲面が一価関数で表せる場合について隠面消去を行ない表示せよ(この場合、制御点のx、yは等間隔で高さzのみ変化させる)。
一価関数のJavaによる隠線表示の例および解説は下記を参照のこと。
Applet例:/~nis/junk/sougou/hidfunc/hidfunc.html (プログラム例, 解説)下図の例は、隠面消去を施した4次のBezier曲面で、制御ネットと曲面上の等パラメータ曲線(一方向のみ)を描画している。
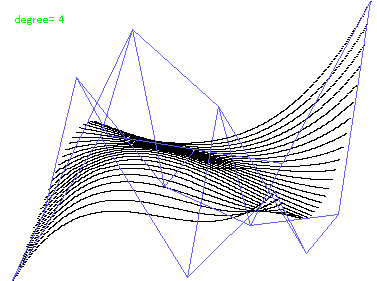
図1
- 任意の4辺形の場合計算が難しいので、平行4辺形あるいは少なくとも2辺が平行なものを考える。4辺形内のある点は4辺形内で定義されるパラメータ(u,v)座標を考え、変形後の4辺形の同一パラメータ座標に移動させる。
- 4辺形内の図形は点、線または多角形で表現されるものとする (あるいは画像でもよい)。
- 図に示すように、スクリーン座標を(x、y)とし、頂点P1、P2、P3、P4からなる4辺形を考える。変換後の4辺形をP1'、P2'、P3'、P4'とする。4辺形内部の任意の点P(x、y)を4辺形内部のパラメータ座標(u,v)で表すと(0<u,v<1)、変形後の4辺形のパラメータ座標(u、v)からP’(x’、y’)を算出する。
なお、P1はu=0、v=0、P3がu=1、v=1に対応する。
基本的には双1次補間の式を用いると任意の点Pとパラメータの関係は次式で表現できる。
P=(1-u)(1-v)P1+(1-u)vP2+u(1-v)P4+uvP3 一般に、P(x,y)から(u,v)を算出する式は複雑なので、2辺(例えばP1P2とP3P4)が平行な場合には簡単な算出式になるので、計算式を導出せよ。
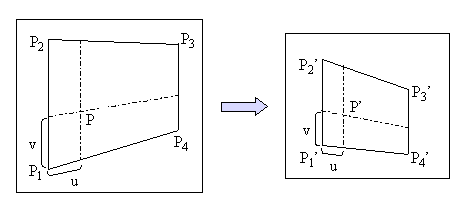
図2 - 可能な人は画像の変形を行いなさい。この場合は、変形後の4辺形を走査し、走査線上のある点P’の(u、v)を計算し、変換前の点P(u、v)の位置の画素の色を
P'の色として描画する。
ここで、変形後の4辺形を走査して、図4のようにスムーズシェーデイングと同じ方法で走査してる点のパラメータ値を算出してもいい(資料[2]参照)。
図4に、P1',P2'からPLを、P3',P4'からPRのパラメータを補間で算出し、PL,PRからPのパラメータを補間で算出できる。

図3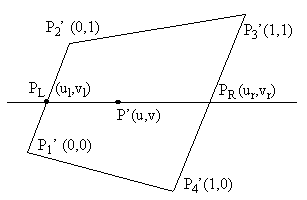
図4課題 4 イメージベースドレンダリングの例として、TIPの考え方を用いて1枚の画像(または投影図形)を異なる方向から見た画像を生成せよ。 下図の左が元の画像で、視点を変えた画像の生成例が右である(資料[3]から引用)。


図5
- 図6に示すように画像にスパイラルメッシュ(消点を画面のほぼ中央におきその点にあつまる放射状の線)を当てはめる。異なる視点からみた画像にするため
消点を移動させる。すなわち、入力画像に新たな消点に対するスパイラルメッシュを当てはめて変形する。

図6 - 画像の読み込みのプログラムが困難な人は、プログラム中で生成する単純な図形でもよい。また、上の図のように近景により背景が隠されるようなこともない例でよい。
- 視点を変更後の4辺形を課題3の方法で塗る。下図のように画像に緑で示される4辺形を割り当て、それがスパイラルメッシュに伴い変形すると考える。

図7 - TIPに関する参考URL
- http://www.cs.unc.edu/~hoff/projects/comp390/tip/
- http://www.cs.virginia.edu/~dbrogan/CS551.851.animation.sp.2000/
- http://graphics.stanford.edu/courses/cs99d-98/online_projects.html
参考資料
- [1] A. Iglesias,"BEZIER CURVES AND BEZIER CURVES AND SURFACES"
- [2] A. Iglesias、"ILLUMINATION MODELS"
- [3] 安生、デジタル映像製作とイメージベース技術
Ⅱ レポート課題- n次のBezier曲線とm次のBezier曲線を乗じるとBezier曲線になることを証明せよ。また、何次の曲線になるか?
- 直線Lとn次Bezier曲線との距離はn次Bzier曲線となることを示せ。
- 曲面のレイトレーシング法についていくつか紹介し比較せよ。
参考- C言語の場合;
これらの課題において、画像をセーブすることが必要になるが、保存の画像形式およびそのプログラムは下記を参考にして下さい。
/~nis/junk/ppm.html - Java の場合;
- Java文法は下記を参照。
/~nis/junk/sougou/document/javaBunpou.htm - Java例題
- (1) Javaの図形基本要素を組み合わせた例: Applet例 プログラム例
- (2)矩形領域内を補間法で塗る例: Applet例2
- (3) ブレゼンハムの直線描画法の例: Applet例, プログラム例、 解説 (直線を描くコマンドが無い場合に、直線を描く場合、直線上の画素を走査するようである。その際不可欠な方法)
- CG関係のJava Aplet例
- (1) Javaの図形基本要素を組み合わせた例: Applet例 プログラム例
- Java文法は下記を参照。
- http://www.cs.unc.edu/~hoff/projects/comp390/tip/
- 図6に示すように画像にスパイラルメッシュ(消点を画面のほぼ中央におきその点にあつまる放射状の線)を当てはめる。異なる視点からみた画像にするため
消点を移動させる。すなわち、入力画像に新たな消点に対するスパイラルメッシュを当てはめて変形する。