コンピュータグラフィックス論課題

2005 2.2訂正

Ⅰ プログラミング課題

下記のプログラミング課題において４問中少なくとも３問を提出せよ。

インタラクティブ性のあるプログラムが理想であり、それを遠隔地でも評価するにはJavaで作成すると効果的であるので、可能な人はできるだけJavaAppletを試みて下さい（この場合画像サイズは300ｘ300以下でもよい）。Ｃ言語とOpenGLを用いて表示する方法でもよい。この際、出力例がカラー画像の場合、それを評価して欲しい人は、自分のホームページに画像を置いて見れるようにしてもよい。
注；　誤字等があれば訂正するので、このページを更新するので再度確認して課題を提出してください。
/~nis/junk/lecture/VisRep05.html

課題１ Bezier曲線、Bスプラインの描画プログラムを作成せよ。

３次の曲線を描画する。曲線の式は資料[1]を参照のこと。
次数は３に制限してよいが、制御点の数は可変（例えば５から８）にする。
次数を1つ上げて、まったく同じ曲線を制御点とともに表示せよ。
曲線を2分割し、それらの制御点と曲線を表示せよ。 (分割法参照 )
Bスプライン曲線を描画する。曲線の式は資料[2]を参照のこと。
下記URLのアプレットを参照せよ。 /~nis/javaexampl/bspline.htm

課題2 波揺れる水面をシミュレートし可視化するプログラムを作成せよ（配布資料[2]参照）。

100x100の配列を準備し、資料[2]p.2のフーリエ級数の式（10）、または波動方程式（13）を差分化した式（15）を用いて波の高さをシミュレートせよ。　
水面を任意の位置から見た線画で表示するか（透視変換参照）。あるいは、水面を多角形で表示された物体として捉え反射のみを考えて水面の陰影付け、図１のように三次元状に水面を表示せよ。水面を表示するには、多角形メッシュで波面を表す方法でもいいし、バンプマッピング（資料[4]参照）で法線を揺らして表現するのでもいい。
計算結果は静止画像で保存するか、可能な人は図１右のようなマウスをクリックしたら波が立つようなインターフェースを持つプログラムを作成せよ（陰影の計算は参照資料[3]参照）。

図１　水面波の表示例　左：海面の表示　右：インタラクティブに水面に波をおこす

課題3 2次元空間でテクスチャマッピングを行うプログラムを作成せよ（配布資料[4]参照）。

最初に画像データをプログラムで読み込み色データの配列を記憶する。画像読み込みができないときには、縞模様やチェック模様などの簡単なものをプログラム内で作成してもかまわない。テクスチャーを自分で生成する場合、マンデルブロー集合やフラクタルで生成してもよい（資料｢3｣参照）。
次に4点を指定し、それを囲む4角形内部にテクスチャの頂点と、指定した4角形の頂点を一致させ4角形内部も描画する。このとき4角形がねじれる場合は考慮しなくてよい。
指定4角形内部の描画のためには、テクスチャのピクセルに最も近い座標の色をコピーする最近点サンプリング、またはテクスチャのピクセルに最も近い点の上下左右にあるピクセルの加重平均を計算する線形フィルタリングを用いよ。

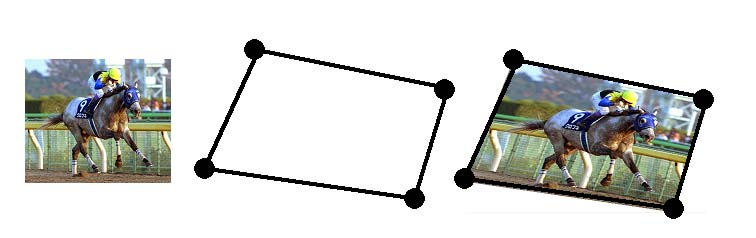
図2　テクスチャマッピング　左：用意した元テクスチャ　真中：4点を指定　右：指定した４点による４角形にテクスチャをマッピング

課題4　３次元ボリュームデータのレンダリングを行うプログラムを作成せよ（配布資料[6]参照）。　

例えば卵の白身と黄身のような外と中身で違いがあり半透明レンダリングの効果が見える3次元ボリュームデータを用意して、各ボクセルの色と不透明度を考慮してボリュームレンダリングを行え。
視点変更や不透明度をインタラクティブに変更できるインターフェースを作成せよ。

JavaやX-windowの使用方法を勉強する時間のない場合は、次の方法でもよい。すなわち、スクリーンを想定した配列を準備し、それに輝度情報を書き込み、準備したツールで可視化する。画像サイズは500ｘ400程度とする。ただし、プログラムリストと結果のハードコピー（PostScript形式にしプリント）を提出すること。この際、画像をセーブすることが必要になるが、保存の画像形式およびそのプログラムは資料を参考にして下さい。

注：プログラミングが困難な学生は相談に応じてレポート課題を提出する方法も考慮します（メイルしてください）。

参考資料(配布資料)
[1] A. Iglesias, "BEZIER CURVES AND SURFACES"
[2] A. Iglesias, "BSpline　and NURB CURVES AND SURFACES"
[3] 西田　「CG数理；自然物レンダリング」
[4]　A. Iglesias, "TEXTURE AND BUMP MAPPING"
[5]　A. Iglesias, "ILLUMINATION MODELS"
[6] C.Bajaj "An Introduction to Computational Visualization"

Ⅱ　レポート課題

放物線を2次の有理Bezier曲線で表す場合、制御点と重みを算出する式を求めよ(資料[1]参照)。
2次のBezier曲面Cと直線Lとの交点を算出する式を導出せよ。また、交点での法線を算出せよ。
ボリュームデータの可視化の方法にMarching Cubesという方法があるが、この方法について説明し、長所欠点を述べよ。
　Ａ－Pachesとは何か説明せよ（資料[6]参照）

参照URL

締切：　２月１７日（木曜）　結果は各自のホームページに置くか、印字して事務室に提出、あるいはメイルに添付して下さい。

連絡先：email: nis@is.s.u-tokyo.ac.jp 電話: 内線24106 (西田研究室）: /~nis/　

コンピュータグラフィックス論 課題

コンピュータグラフィックス論課題