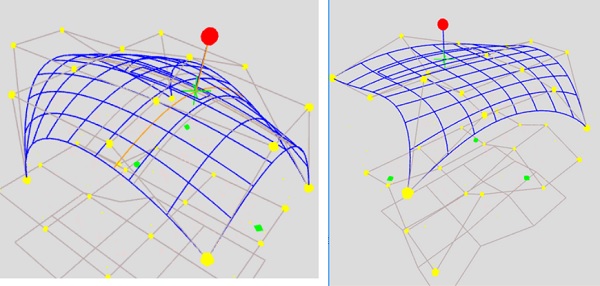
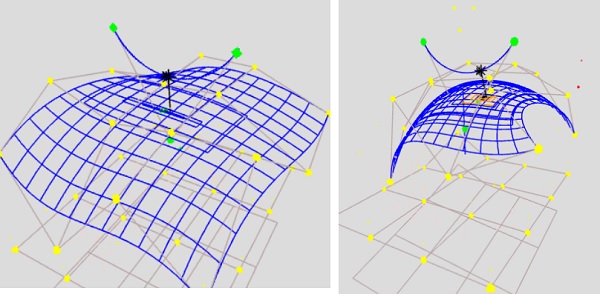
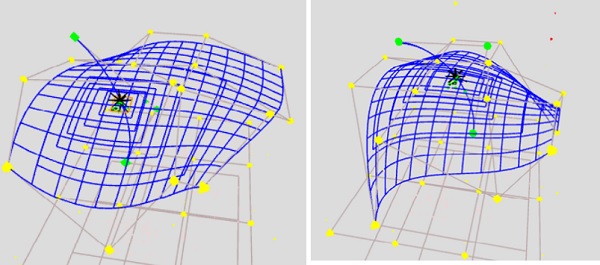
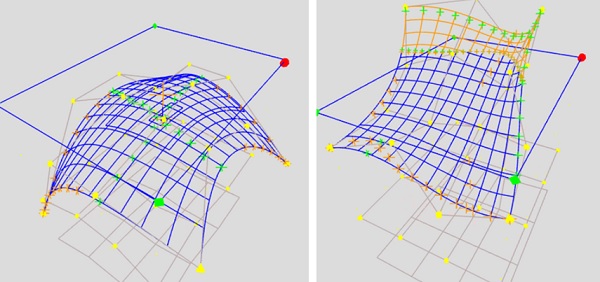
- Nishita、「Educational and Research Applications of Generative AI–Assisted Development of Various Computer Graphics Programs」,IEVC2026
, 2026-3 、keynote Hiroshima
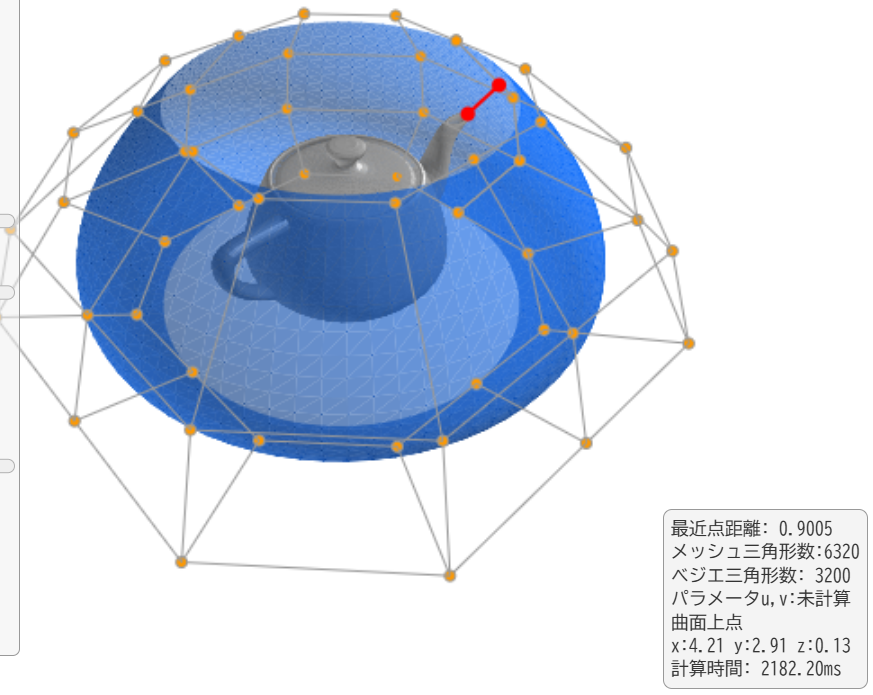
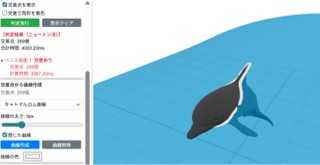
- 西田、「三角形メッシュ形状とBスプライン曲面との最近点計算」,IPSJ全国大会2026
, 2026-3 、松山大学 文京キャンパス
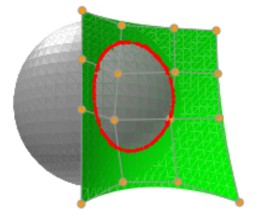
- 西田、「三角形メッシュ形状とベジエ曲面の距離関数を用いた交差計算」,映像表現・芸術科学フォーラム
, 2026-3,東京工芸大学中野キャンバス
- 西田、「三角形メッシュ形状とNURBS曲線との干渉計算を考慮した曲線編集」,Nicograph 2025
, 2025-9 広島
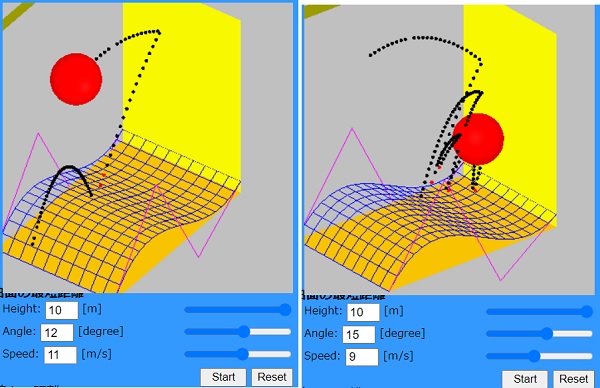
- 西田、「生成AIの支援による多種のCGプログラム作成の体験学習」,
映像表現・芸術科学フォーラム, 2025-3
- 西田、「距離関数と分割法を用いたnurbs曲線の交点計算」、 (nicograph2024) 、2024-11、
原稿〆8/5
- 西田、中村、「距離関数を用いたBスプライン曲線の交差および近接判定」、Visual Computing 2024 、2024-9 東洋大学 9/11
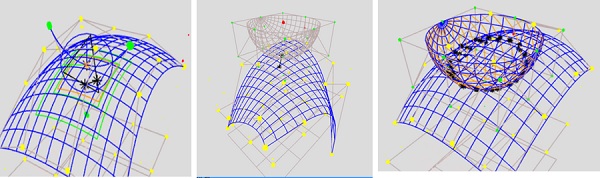
- 西田、「距離関数と包含球を用いた3次元Bスプラインの編集」、第23回情報科学技術フォーラム (FIT2024) 、2024-9、広島工大 9/4
- 西田、「距離関数を用いたNURBS曲線と線分の交差および最近距離の計算」、画像電子年次大会 2024 、2024-8 長崎 8/28
- 西田、中村、「距離曲線を利用したベジエ曲線・曲面の包含球の計算と交差判定」映像情報メディア学会研究会、2024-3 映情学技報, vol.48, pp. 280-283 、
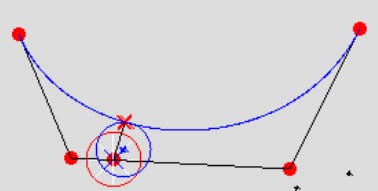
- 西田、「ベジエ曲線の距離関数を用いたベジエ曲線・曲面の包含球の計算法」、情報処理学会第86回全国大会、2024-3, 7c-01
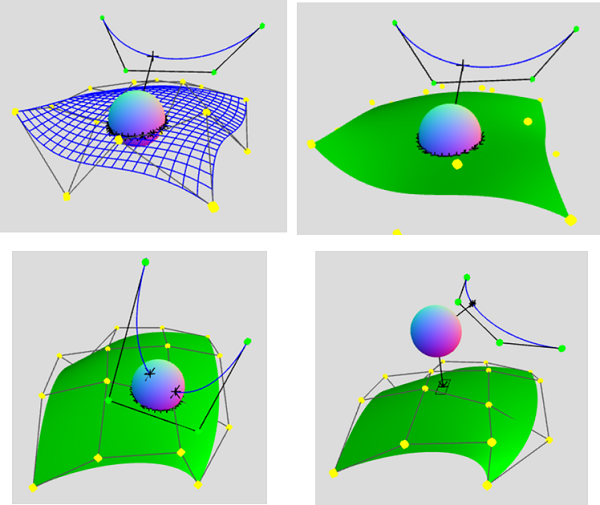
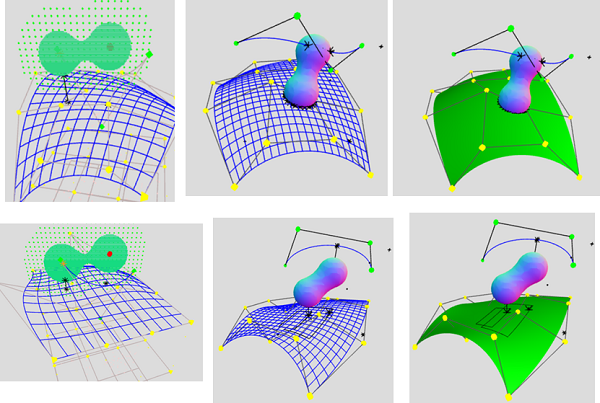
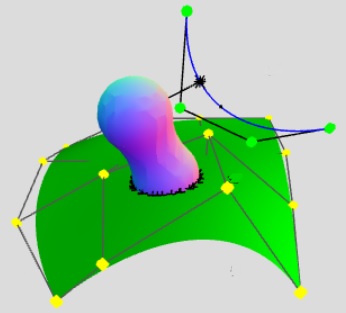
- T.Nishita, Y.Nakamura "Collision Detection between Spheres and B-spline Surfaces using Distance Functions from Curves", Nicograph International 2023, 2023-6, ieee
- 西田、「曲線からの距離関数を用いた球とBスプライン曲面の衝突判定」GCAD研究会、ポスター(スポットライト)、2023-2‐27
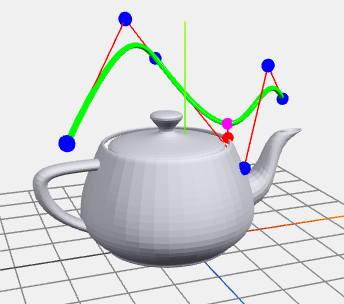
- 西田、「最近点検出による3次元ベジエ曲線・Bスプラインの編集」、情報処理学会 第85回全国大会、2023-3, 5c-06 pdf
- 西田、「レイマーチング法による円柱曲面・オフセット曲面の表示」, VC+VC2022 , 19(short) ,
2022-10,
- 西田、「 Bezier曲線からの距離場を利用したフィールドモーフィング」、第50回画像電子学会年次大会,
G1-1 #45、2022-9
- 西田、「曲線からの距離関数を用いたレイマーチング法の開発」、 情報処理学会第84回全国大会、6E05,2022-3、 pdf
- 西田、「有理ベジエ曲面と球やメタボールの干渉計算」、芸術科学会論文誌 Vol.20, No.4,
pp.204-209、2021-11 pdf
- 西田、「分割法を用いた有理ベジエ曲線・曲面の間隙計算」,VC+VC2021, 36(short),
2021-9
- 西田、「有理ベジエ曲線・曲面間の最短距離検出法」、第20回情報科学技術フォーラム(FIT2021)、I-012、
2021-8
- 西田,出本,「曲面と多角形との最短距離検出法」、Visual Computing / グラフィクスと
CAD 合同シンポジウム, 2017-6
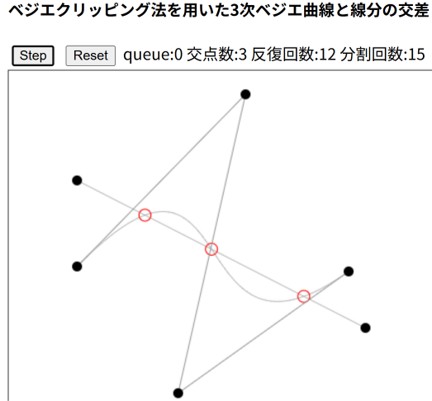
- 西田,「ベジエクリッピング法を用いた曲面と平面との最短距離計算法」,情報処理学会全国大会,2016-9
IIPSJmarch.pptx,
IPSJ23edit.pptx,
nico21gap.pptx,
cgvSpot.pptx,
FIT21gapFinal.pptx,
BezClipt.ppt,
IPSJ2024nis.pptx,
Forum24nis.pptx,
MCC24nurb.pptx,
IPSJ24Clind.pptx,
FIT24Bspline.pptx,
VC24Bspline.pptx,
nico24nurb.pptx,
|
??
??
??
paper
paper
paper
paper
paper
|
nico24nurb.pptx
??
??
ppt
ppt
ppt
ppt
|