コンピュータグラフィックス論 課題（2012年度）

• 走査線と多角形との交点計算は増分法を使用する。
• ｎ多角形とし、対話的に頂点はマウスで入力するかファイルから読むこととする。 下記の課題に使用するために３角形に限ってもよい。
• 多角形内の色は次の2種とする。１）同一色,２）各頂点の色（輝度）を与え内部は線形補間する（補間にはスムーズシェーディング法を使用すること）。 ３角形の場合、各頂点をR,G,Bの色を割り当てる。

課題２ Bezier曲線の描画プログラムを作成せよ。

• 任意の次数の曲線を描画する。参考；Bezier曲線の分割>を利用すると演算量がすくない。
• 複数の曲線をスムーズに結合して曲線形状を表現しなさい。 次数は３に制限してよいが、 例として、複数のBezier曲線を組み合わせて円（真円でなくてよい） 、アウトラインフォントなどを描画せよ。

課題 3 ３次元フォーマットのファイルを読み込み、表示するプログラムを実装せよ。 wavefront(.obj), collada(.dae), Metasequoia(.mqo)などがわかりやすく他にもmaya(.mb) lightwave(.lw), autodeskFBX(.fbx), MMD(.pmd)などのバイナリファイルなどに挑戦してみても良い。なお、OpenGLやDirectX、enchantjsの使用を推奨する。
【必須条件】

• 頂点の３次元座標および面（法線ベクトルもある場合がある）の読み込みを行うこと。
• ワイヤーフレームでも面表示でも良い。
• wavefront(.obj)フォーマットはhttp://en.wikipedia.org/wiki/Wavefront_.obj_fileで定義されている。
• wavefront(.obj)ファイルのサンプルはこちらUtahのteapot
• 表示した形状ファイルも添付すること。

• 光源を指定し、陰影が表示されていることを確認すること
• カメラ、もしくは物体を移動できるようにすること
• 色やテクスチャの読み込み

課題 4 レイトレーシングを実装し、球などの形状の描画をせよ。

• 反射・屈折のすくなくとも一つを組み込むこと。
• 球自体が反射・屈折する必要はなく平面鏡などを設置してもよい。

• 形状に関しては球・箱・任意形状のいずれでもよい。(球が一番簡単。課題3と組み合わせても良い）
• 屈折率は任意に変更できるようにすること。(外部ファイルでも引数でも対話的でもよい。)

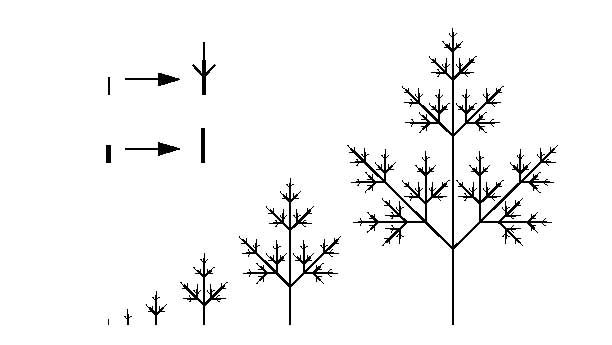
課題 5 フラクタル(自己相似性)を用いた形状の表示をせよ。フラクタルについては教科書86P〜89Pを参考にすること。

• 面表示でもワイヤーフレーム表示でも良い。
• コッホ曲線や山岳形状、木構造の表示、リアス式海岸の表示など好きなものを選ぶこと。
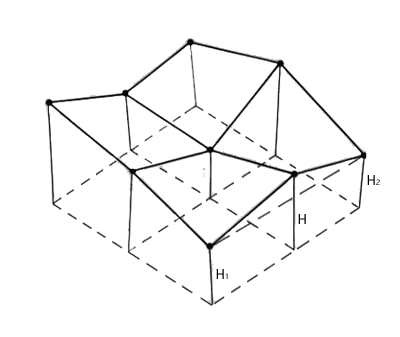
• 山岳形状の場合には教科書pp.88〜89で紹介されている中点変位法を参考にせよ（下図は4辺形を4分割し、各辺の中点を変位させた例）。
• パラメータを対話的（ＵＩを利用）に任意に変更できるとなおよい（オプション）。

参照URL

• Java文法; /~nis/junk/sougou/document/javaBunpou.htm
• Javaプログラム例解説: /~nis/junk/sougou/document/javaKadai.htm
• Java Applet集; /~nis/javaexampl/javaExmpl.shtml
• CG関連図書: /~nis/junk/cg_books.html

締切：　8月17日（金曜）17：00! 　(なお期限に遅れた人は9月14日(金曜)には提出のこと（ただし評価にハンディはある）. また enchant.jsを利用した課題に関しては、８月４日までに送ってください。優秀なものは米国での講演で紹介します。

課題はメールで提出とします。メールのタイトルは『【CG論課題】-学籍番号-名前-解いた問題の番号と使用言語(Library)』としてください
例『【CG論課題】-********-東大 花子-1(Java),2(C++),3(gl.enchant.js),4(ocaml),5(scheme)』
結果(プログラムソース、実行形式、結果画像、レポート）は、各自のホームページに置いて本文にリンクを貼る、もしくはメールにファイルを添付して送って下さい。

連絡先：email: nis@is.s.u-tokyo.ac.jp /~nis/　
メイルはＴＡの今井 etoile@nis-lab.is.s.u-tokyo.ac.jp にもccして下さい。